|
|
Introduction
This package contains container classes for parameter related data, e.g.
parameter points. All classes are child-classes of
ParameterBase, which itself inherits from
numpy’s ndarray. Methods exist for IO to/from dict and text files:
The following classes are implemented:
- ParameterPoint
- Container for name-value data, e.g. locations or directions in
parameter space.
- ParameterRange
- Container for name-val1-val2 data, e.g. parameter ranges for
sampling anchor points or line-scan points.
- ParameterErrors
- Container for errors of tuned parameter values.
- ParameterMatrix
- Container for parameter-parameter matrix data, e.g. the correlation
matrix.
Documentation
-
class professor.params.base.ParameterBase
Bases: numpy.ndarray
Base class for name-value kind of containers.
- Factory functions for easy instance creation are:
- mkFromDict()
- mkFromFile()
The constructor takes two arguments:
- names : array_like
- The parameter names.
- values : array_like
- The parameter values.
Methods
-
asDict()
Convert the data to dict.
The keys are the parameter names the values the stored numerical
data.
The resulting dictionary is suitable to create a new instance with
mkFromDict().
-
dim
-
format(key=None, sep=' ')
Format parameter names and values.
The default format is:
Par1 val1 val2 ...
Par2 ...
Numbers are formatted using %e.
| Parameters : | key : function, optional
Comparison function used to sort parameter names with the
builtin sorted function. Use None to preserve
the order of names
sep : str, optional
String used to separate parameter names and values.
[default: two spaces]
|
|---|
-
getIndex(name)
Return the index of parameter name.
-
keys()
Get the parameter names.
Implemented for dict-like behaviour:
>>> d = dict()
>>> params = ParameterBase(["a", "z"], [1.3, 9e4])
>>> d.update(params)
>>> d
{'a' : 1.3, 'z' : 90000.0}
-
classmethod mkFromDict(d)
Create an instance from a dictionary.
| Parameters : | d : dict
For 1D parameter data, e.g. parameter points
d must have the form:
d = {"PAR1" : val1, "PAR2" : val2 }
for other data types, e.g. parameter errors and ranges:
d = {"PAR1" : [val1, val2],
"PAR2" : [val3, val4] }
In principle nesting is allowed, resulting in 3+ dimensional
arrays.
|
|---|
-
classmethod mkFromFile(path)
Load parameters from a file.
| Parameters : | path : str
The path of the file.
|
|---|
-
names
The parameter names.
Warning
The names are stored in an numpy.ndarray as instances of numpy.string_.
-
writeParamFile(path, key=None)
Write the return value of format() to a file.
-
class professor.params.ParameterPoint
Bases: professor.params.base.ParameterBase
-
format(key=None, sep=' ')
Format parameter names and values
- The format is::
- Par1 val1
Par2 val2
...
Numbers are formatted using %e.
| Parameters : | key : function, optional
Comparison function used to sort parameter names with the
builtin sorted function. By default
professor.tools.sorting.cmpByInt() is used to sort
parameter names by a contained number.
sep : str, optional
String used to separate parameter names and values.
[default: two spaces]
|
|---|
-
classmethod mkFromString(s)
Create an instance from a string.
Typical use-case is parsing of command line option.
| Parameters : | s : str
A string with parameter names and values of the form
“Name1=Val1,Name2=Val2”.
|
|---|
-
class professor.params.ParameterRange
Bases: professor.params.base.ParameterBase
Container for parameter ranges.
Range definitions are stored as low and high bounds for each parameter.
I.e. a range is given by two parameter points.
- Possible use cases are:
- Ranges of anchor points that are used for an interpolation.
- Ranges for random point sampling.
- Ranges for line-scan point sampling. The line is given by the
diagonal stretching between the two corner points of the parameter
range.
Warning
The low and high properties contain the corners of the parameter
range. They will not always fulfill 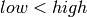 . This is especially
the case with line scans. . This is especially
the case with line scans.
Examples
Create a parameter range and sample randomly from it. Parameter “Par1” is
in [0.0, 1.0], “Par2” in [3.5, 3.6]:
>>> range_ = ParameterRange(["Par1", "Par2"], [[0.0, 1.0], [3.5, 3.6]])
>>> # Get a 2D random point in [0.0, 1.0].
>>> rndpoint = np.random.rand(2)
>>> # Convert it to the cube defined by range_
>>> range_.getRelativePoint(rndpoint)
Create a parameter range and sample along the diagonal, as one would do
for a line scan:
>>> range_ = ParameterRange(["Par1", "Par2"], [[0.0, 1.0], [3.5, 3.6]])
>>> for rel in np.linspace(0.0, 1.0, 10, endpoint=True):
>>> print range_.getRelativePoint(rel)
# some out put
or get the same points in one numpy.ndarray:
>>> relative = np.linspace(0.0, 1.0, 10, endpoint=True)
>>> range_.getRelativePoint(relative[:,np.newaxis], plainarray=True)
array([[ 0. , 3.5 ],
[ 0.11111111, 3.51111111],
[ 0.22222222, 3.52222222],
[ 0.33333333, 3.53333333],
[ 0.44444444, 3.54444444],
[ 0.55555556, 3.55555556],
[ 0.66666667, 3.56666667],
[ 0.77777778, 3.57777778],
[ 0.88888889, 3.58888889],
[ 1. , 3.6 ]])
Methods
-
center
Calculate the center of the spanned hyper cube.
| Returns : | center : ParameterPoint |
|---|
-
diagonal
Calculate the diagonal of the spanned hyper cube.
| Returns : | diag : ParameterPoint |
|---|
-
getNormalisedPoint(x, plainarray=False)
Transform x to normalised coordinates in ranges.
If x is inside the ranges the returned values will be between 0
and 1. This is the inverse function of getRelativePoint().
| Parameters : | x : array_like
plainarray : bool
Do not cast the returned value back to a ParameterPoint.
Useful if x has shape (1, numpoints). The returned array has
then shape (dim, numpoints).
|
|---|
| Returns : | new : ParameterPoint, ndarray
A ndarray is returned if plainarray is set.
|
|---|
-
getRelativePoint(x, plainarray=False)
Transform normalised x to ranges.
x is expected to have normalised values. Values of x[i] = 0.0
and `x[i] = 1.0 correspond to the first and second corner of the
parameter range, respectively.
This can be useful to construct random points from this parameter range:
>>> range_.getRelativePoint(np.random.rand(pr.dim))
| Parameters : | x : array_like
plainarray : bool, optional
If True do not cast the returned value back to a
ParameterPoint. Useful if x has shape (1, numpoints).
The returned array has then shape (dim, numpoints).
The defalt is to return a ParameterPoint instance.
|
|---|
| Returns : | new : ParameterPoint, ndarray
A ndarray is returned if plainarray is True.
|
|---|
-
high
-
isInside(point)
Return True if point is inside the ranges.
-
low
-
classmethod mkFromPoints(points)
Create a parameter range spanned by a list of points.
The range is then defined by the min/max values in each direction.
-
classmethod mkFromString(s)
Create an instance from a string.
Typical use-case is parsing of command line option.
| Parameters : | s : str
A string with parameter names and values of the form
“Name1=Low1=High1,Name2=Low2=High2”.
|
|---|
-
class professor.params.ParameterErrors
Bases: professor.params.base.ParameterBase
-
class professor.params.ParameterMatrix
Bases: professor.params.base.ParameterBase
Class for parameter-parameter matrix data, e.g. correlations.
An instance can be easily created from a dictionary with
mkFromDict().
The item look-up is modified to allow to specify the matrix cell by two
parameter names:
>>> d = { ("PAR1", "PAR1") : 11 ,
... ("PAR1", "PAR2") : 12 ,
... ("PAR2", "PAR1") : 21 ,
... ("PAR2", "PAR2") : 22 }
>>> matrix = ParameterMatrix.mkFromDict(d)
>>> matrix["PAR1", "PAR2"]
12.0
>>> matrix["PAR1", "PAR2"] = 120
>>> matrix["PAR1", "PAR2"]
120.0
Methods
-
asDict()
-
classmethod mkFromDict(d)
| Parameters : | d : dict
A mapping of tuples of parameter names on matrix values, e.g.:
d = { ("PAR1", "PAR1") : val_11 ,
("PAR1", "PAR2") : val_12 ,
("PAR2", "PAR1") : val_21 ,
("PAR2", "PAR2") : val_22 }
|
|---|
|
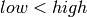 . This is especially
the case with line scans.
. This is especially
the case with line scans.